Demystifying AlexNet: A Step-by-Step Guide to Understanding the Pioneering CNN - Part 1

Exploring the architecture and historical impact of AlexNet, the revolutionary convolutional neural network that kickstarted the deep learning era in computer vision.

Introduction

In the rapidly evolving realm of artificial intelligence, certain breakthroughs not only push boundaries but completely redefine them. Ever wondered how machines can truly see the world? In the field of computer vision, one such landmark moment came with the introduction of AlexNet in 2012—a model that revolutionized how machines interpret and understand visual data.

This mini-series delves into the architecture, innovations, and long-lasting impact of AlexNet, a model that opened the floodgates for deep learning in computer vision. But it’s not just about one algorithm—it's about the transformation of how AI perceives and processes the world, sparking advancements that continue to shape industries today.

In Part 1, we’ll explore the foundation upon which AlexNet was built, dissect its internal workings, and explain how its novel design overcame previous challenges. By understanding its architecture, you’ll gain insights into how this model paved the way for future innovations in the field.

In Part 2, we’ll go hands-on. You'll see how to implement AlexNet using PyTorch, walking through the code step by step, and learning how to train it from scratch—empowering you to harness its capabilities for your own projects.

History of AlexNet

In 2012, the field of computer vision stood at a crossroads. The ImageNet Large Scale Visual Recognition Challenge (ILSVRC) had been pushing researchers to improve object classification and detection in a vast dataset of over a million images. However, traditional methods, relying heavily on hand-engineered features, seemed to be approaching their limits with top-5 error rates plateauing around 26%.

At that time, a University of Toronto-based team developed AlexNet—named after Alex Krizhevsky, who created it along with Geoffrey Hinton and Ilya Sutskever. This groundbreaking convolutional neural network, at the time called SuperVision, not only won the ImageNet Large Scale Visual Recognition Challenge (ILSVRC), it also achieved unprecedented accuracy in image recognition tasks and also once again sparked a wider interest in deep learning research and applications for vision models.

AlexNet's 2012 breakthrough and subsequent improvement compared to contemporary models [1]

AlexNet's release marked a pivotal moment in AI history. Leveraging the growing power of GPU computing, the team trained a deep convolutional neural network of unprecedented scale - 60 million parameters and 650,000 neurons. When unveiled at the 2012 ILSVRC, AlexNet shattered existing performance benchmarks with a top-5 error rate of just 15.3%, outpacing its nearest competitor by an astonishing 10 percentage points. AlexNet's success, perfectly timed with the convergence of big data, improved computing power, and refined neural network techniques, ushered in a new era of AI research for vision models.

Understanding AlexNet

After introducing AlexNet, let's take a closer look at its core components to understand how it functions. AlexNet is a specific implementation of a convolutional neural network (CNN), notable for its use of deeper layers, large datasets, and GPU acceleration. Its architecture comprises layers such as convolutional layers, which detect features, pooling layers that reduce dimensionality, activation functions like ReLU that introduce non-linearity, and fully connected layers that make final predictions.

To grasp AlexNet fully, it’s essential to understand CNNs themselves. CNNs are built with sequential layers that perform key operations: convolution for feature extraction, pooling for downsampling, and fully connected layers for classification. AlexNet capitalized on these concepts, but its innovations in depth and computational efficiency set it apart.

1. Convolutional Layers

Anatomy of a Convolutional Layer: From RGB Input to Feature Maps

Function

Convolutional layers are fundamental components in Convolutional Neural Networks (CNNs). They apply filters (also called kernels) to the input data, typically images. These layers are designed to automatically and adaptively learn spatial hierarchies of features from low-level patterns (like edges and textures) to high-level concepts (like shapes and objects).

AlexNet implementation

96 convolutional kernels of size 11×11×3 learned by the first convolutional layer on the 224×224×3 input images. The top 48 kernels were learned on GPU 1 while the bottom 48 kernels were learned on GPU 2. [6]

In the original AlexNet architecture, the first convolutional layer utilized 96 convolutional kernels (filters) of size 11×11×3 to process input images with dimensions of 224×224×3 (height, width, and RGB channels). These filters were designed to capture low-level features such as edges, textures, and color gradients from the input images. The network was parallelized over two GPUs, with the top 48 filters being learned by GPU 1, and the bottom 48 filters being learned by GPU 2. This parallel training setup helped AlexNet efficiently handle the computational load, speeding up the training process for large-scale datasets like ImageNet.

The filters learned by the first layer exhibit a variety of visual patterns. Some are edge detectors, sensitive to specific orientations, while others are color filters, capturing different hues and textures. The figure showcases this diversity: the filters on the top row mainly focus on capturing edges in different orientations and intensities, whereas the bottom row displays filters that are more attuned to color contrasts and finer details. This initial layer is critical in extracting essential visual patterns, which subsequent layers of the network further process to detect more complex features like shapes and objects.

Math behind it

The core operation in convolutional layers is a sliding dot product:

1. The kernel (a small matrix of weights) slides across the input data.

2. At each position, an element-wise multiplication between the kernel and the current input patch is performed.

3. The results are summed to produce a single value in the output feature map.

4. This process is repeated for every possible position of the kernel over the input.

Mathematically, for a 2D convolution:

\(\begin{equation} (f * g)(x, y) = \sum_{m=-k}^{k} \sum_{n=-k}^{k} f(x+m, y+n) g(m, n) \end{equation}\)

Components:

• f: Input (e.g., an image)

• g: Kernel or filter

• (x, y): Output coordinates

• (m, n): Kernel coordinates

Effectiveness

Convolutional layers are particularly effective for processing data with grid-like topology (e.g., images) for several reasons:

1. Spatial Locality: They exploit the strong local spatial correlations present in natural images. The assumption that nearby pixels are more related than distant ones holds true for most real-world images.

2. Hierarchical Feature Learning: By stacking multiple convolutional layers, the network can learn increasingly abstract and complex features. Early layers might detect edges and simple textures, while deeper layers can recognize complex shapes or entire objects.

3. Translation Invariance: The same kernel is applied across the entire image, allowing the network to detect features regardless of their position in the image.

4. Reduced Parameters: Compared to fully connected layers, convolutional layers have significantly fewer parameters due to weight sharing and local connectivity.

Parameter Sharing

Parameter sharing is a key concept in convolutional layers:

1. Principle: Each filter is applied across the entire input, using the same set of weights at every position.

2. Benefits:

   • Drastically reduces the number of parameters compared to fully connected layers.

   • Improves generalization by forcing the model to learn position-invariant features.

   • Allows the network to process inputs of varying sizes.

3. Implications: A feature detected in one part of the image can be recognized anywhere else, promoting translation equivariance.

2. Pooling Layers

Comparison of Max Pooling vs. Average Pooling using a 2x2 filter on a 4x4 input grid [2]

Function

Pooling is essential in convolutional neural networks (CNNs) as it reduces the spatial dimensions of feature maps, lowering computational complexity and preventing overfitting. It introduces translation invariance by summarizing local features, enabling the detection of important patterns regardless of their position in the input. Pooling also expands the receptive field of neurons in deeper layers, capturing hierarchical data patterns. AlexNet, benefited from max pooling by efficiently managing large images, selecting key features, and enhancing the network’s ability to recognize objects despite transformations, contributing to its success in the 2012 ImageNet competition.

Math behind it

The core operation in pooling layers is a sliding window function:

1. A window (typically 2x2 or 3x3) slides across the input data.

2. At each position, a summary statistic of the values in the window is computed.

3. This summary value becomes a single entry in the output feature map.

4. This process is repeated for every possible position of the window over the input.

Mathematically, for a 2D max pooling operation:

\(\begin{equation} \text{Output}(i,j) = \max_{m \in [i \cdot s, i \cdot s + k], \\ n \in [j \cdot s, j \cdot s + k]} \text{Input}(m,n) \end{equation}\)

Components:

• Output(i,j): The result of the pooling operation at position (i,j) in the output feature map

• Input(m,n): The value at position (m,n) in the input feature map

• i, j: Coordinates in the output feature map

• m, n: Coordinates in the input feature map

• s: Stride of the pooling operation

• k: Size of the pooling window

• max: The maximum function, selecting the largest value within the defined range

• [i·s, i·s+k]: The range of m values in the input feature map for the current pooling window

• [j·s, j·s+k]: The range of n values in the input feature map for the current pooling window

Effectiveness

Pooling layers are particularly effective in CNNs for several reasons:

• Dimensionality Reduction: They reduce the spatial size of the representation, decreasing the amount of parameters and computation in the network.

• Translation Invariance: By summarizing features in a local region, pooling makes the network more robust to small translations in the input.

• Hierarchical Feature Learning: Pooling allows subsequent convolutional layers to operate on a coarser resolution, effectively increasing their receptive field.

• Computational Efficiency: By reducing the size of feature maps, pooling layers decrease the computational load for subsequent layers.

Types of Pooling

As seen on the picture in the beginning of this section.

There are several types of pooling operations, each with its own characteristics:

1. Max Pooling:

   • Operation: Selects the maximum value from the pooling window.

   • Benefits:

     • Preserves the strongest features

     • Provides better translation invariance

   • Drawbacks: Can be sensitive to noise

2. Average Pooling:

   • Operation: Computes the average of all values in the pooling window.

   • Benefits:

     • Preserves background information

     • Can be more stable than max pooling

   • Drawbacks: May dilute strong feature activations

3. Global Pooling:

   • Operation: Applies pooling across the entire spatial dimensions of the input.

   • Benefits:

     • Dramatically reduces parameters

     • Provides invariance to input size

   • Drawbacks: Loses all spatial information

3. Activation functions

Various different activation functions now commonly found in ML models [3]

In general there are many different activation functions, as can be seen in the image above. Covering them all would be an entire article on it’s own, so we’ll now look at and cover the stuff related to the architecture of AlexNet. Activation functions play a crucial role in introducing non-linearity to the model, allowing it to learn complex patterns and relationships in the data. The most significant innovation in this area was the use of the Rectified Linear Unit (ReLU) activation function.

ReLU (Rectified Linear Unit)

Graph of the ReLU activation function [3]

Function

The ReLU activation function is a simple yet powerful non-linear function that has become a staple in modern deep learning architectures. Its widespread adoption began with AlexNet, which demonstrated its effectiveness in training deep neural networks.

Math behind it

Mathematically, it outputs zero for all negative inputs and returns the input value for any positive input. This piecewise linearity introduces non-linearity in neural networks, which helps in learning complex patterns. ReLU is computationally efficient because of its simplicity and avoids the vanishing gradient problem that occurs in other activation functions like sigmoid and tanh. However, it can suffer from the "dying ReLU" problem, where neurons can become inactive if they consistently output zero.

ReLU is defined mathematically as:

\(f(x) = \max(0, x)\)

In other words:

- If x > 0, the output is x

- If x ≤ 0, the output is 0

Effectiveness

ReLU offered several advantages over previously popular activation functions like sigmoid or tanh:

• Sparsity: ReLU can output true zero values, leading to sparse activations. This sparsity is beneficial for both computational efficiency and representational power.

• Reduced Vanishing Gradient Problem: Unlike sigmoid or tanh, ReLU doesn't squash inputs in the positive region, allowing gradients to flow without attenuation when x > 0.

• Computational Simplicity: ReLU involves simple thresholding operations, making it computationally efficient compared to exponential operations in sigmoid or tanh.

• Biological Plausibility: ReLU's behavior is more similar to the firing of biological neurons, which are often silent and only activate when input crosses a certain threshold.

Impact on AlexNet

The use of ReLU in AlexNet was groundbreaking. In their paper, Krizhevsky et al. reported that ReLU-based networks trained several times faster than equivalent networks using tanh units. This speed-up was crucial for training a network as large as AlexNet on the vast ImageNet dataset.

Comparison to other functions

Activation functions play a crucial role in neural networks by introducing non-linearity. ReLU (Rectified Linear Unit), used in AlexNet, outperforms earlier functions like Sigmoid and Tanh. To get visual help understanding these functions, refer to the activation functions headline image.

ReLU, defined as f(x) = max(0, x), is computationally efficient and helps mitigate the vanishing gradient problem. It outputs values in the range [0, ∞), allowing for sparse activations. ReLU is generally fast to compute and effective for deep networks.

In contrast, Sigmoid (range (0,1)) and Tanh (range (-1,1)) offer smooth gradients but are more prone to vanishing gradient issues in deep networks. Sigmoid's non-zero centered nature can cause zig-zagging dynamics in gradient updates, while Tanh, being zero-centered, can partly alleviate this issue.

However, both Sigmoid and Tanh saturate and kill gradients when inputs move away from zero, limiting their effectiveness in deep architectures like AlexNet.

Beyond ReLU

While ReLU was revolutionary for AlexNet, subsequent research has led to variants addressing some of its limitations:

1. Leaky ReLU: Allows a small gradient when the unit is not active.

2. Parametric ReLU: Learns the coefficient of leakage.

3. ELU (Exponential Linear Unit): Smoother version of ReLU with negative values.

These variants aim to solve issues like the "dying ReLU" problem, where neurons can become stuck in a state where they never activate.

The success of ReLU in AlexNet paved the way for further experimentation with activation functions, contributing to the rapid progress in deep learning that followed.

4. Fully connected a.k.a dense layers

Visualisation of a simple single fully connected layer neural network model [4]

After the convolutional and pooling layers extract and downsample features, AlexNet employs fully connected layers to perform high-level reasoning and generate the final classification output. This chapter will be much more of a deep down, since it’s extremely important to understand how neurons map n to n and create actual outputs.

Function

Fully connected layers, also known as dense layers, connect every neuron in one layer to every neuron in the next layer.

In AlexNet, these layers are responsible for:

1. Flattening the 3D feature maps into a 1D vector

2. Learning non-linear combinations of high-level features

3. Mapping the learned features to the target classes

Mathematical Operation

The operation in a fully connected layer can be represented as:

\(y = f(Wx + b) \)

Where:

• y: is the output of the layer (a vector).

• f: is an activation function (such as ReLU, sigmoid, etc.).

• W: is the weight matrix, connecting each input feature to every output neuron.

• x: is the input feature vector (a flattened vector of features).

• b: is the bias term.

The equation behind fully connected layers is crucial to understanding the brute-force nature of these layers, as they map learned features to outputs. By connecting every input feature to every output neuron, fully connected layers aggregate and process information from all parts of the input, which allows the model to make final predictions based on all extracted features.

Breaking Down the Equation

1. Input Vector 𝑥

In the context of a neural network, the input vector 𝑥 represents the data that flows into the fully connected layer. It could be the result of previous operations like convolutions, pooling, or flattening.

For example, if you're using a CNN like AlexNet, the output from the last convolutional or pooling layer is flattened into a 1D vector 𝑥, which becomes the input to the fully connected layers.

\(x = [x_1, x_2, \dots, x_n] \)

Where:

• n is the number of features in the flattened input.

2. Weight Matrix W

The weight matrix W is a set of learnable parameters that are used to scale the importance of each input feature. The size of this matrix depends on the number of inputs and the number of output neurons in the layer.

\(W = \begin{bmatrix} w_{11} & w_{12} & \dots & w_{1n} \\ w_{21} & w_{22} & \dots & w_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ w_{m1} & w_{m2} & \dots & w_{mn} \end{bmatrix} \)

Where:

• W is of size (m×n), with m being the number of output neurons and n being the number of input features.

• Each w​ represents the weight between the i-th output neuron and the j-th input feature.

3. Bias Term b

The bias term b is a vector added to the result of the weighted sum. It allows the model to fit the data better by shifting the activation function.

\(b = [b_1, b_2, \dots, b_m] \)

Where:

• b​ is the bias applied to the i-th neuron in the output layer.

4. Linear Transformation

The output before applying the activation function is calculated as:

\(z = Wx + b \)

This is the result of multiplying the weight matrix W by the input vector x, and adding the bias vector b.

5. Activation Function f

After the linear transformation, an activation function f is applied element-wise to the resulting vector z. This introduces non-linearity, enabling the network to model complex patterns.

\(y = f(z) = f(Wx + b) \)

In the case of AlexNet, the ReLU (Rectified Linear Unit) activation function is commonly used:

\(f(z) = \max(0, z) \)

This activation function ensures that only positive values are passed to the next layer, helping the model learn non-linear relationships.

Role in AlexNet

In AlexNet, the fully connected layers come after several convolutional and pooling layers. These layers aggregate the high-level features learned by the convolutional layers and make the final classification decisions.

For example, the last few layers in AlexNet are fully connected layers:

1. The first fully connected layer has 4096 neurons.

2. The second fully connected layer also has 4096 neurons.

3. The final fully connected layer has 1000 neurons (for the 1000 ImageNet classes).

Each fully connected layer follows the equation y = f(Wx + b), with the ReLU activation applied after the linear transformation.

This structure helps the network learn abstract representations of the input data and map those representations to output classes.

Importance in AlexNet

The fully connected layers in AlexNet serve as a crucial bridge between the feature extraction layers and the final classification. They play several important roles:

1. Feature Integration: FC layers combine features from all parts of the image, enabling the model to reason globally about the image content, rather than focusing on local features alone.

2. Non-linear Transformations: By using multiple FC layers with ReLU activations, the network can apply complex, non-linear transformations, allowing it to capture more sophisticated patterns in the data.

3. Output Generation: The final fully connected layer converts the processed features into class probabilities, linking the learned representations to the specific classification task.

Challenges and Solutions

Despite their importance, fully connected layers come with challenges, especially in a large model like AlexNet. Here's how AlexNet addressed them:

1. Overfitting: With millions of parameters, FC layers can easily overfit the training data. AlexNet mitigated this risk by using dropout, a regularization technique that randomly drops units during training to improve generalization. More on this technique in the next chapter.

2. Computational Cost: Since FC layers contain most of the model's parameters, they are computationally expensive. AlexNet overcame this hurdle by leveraging GPU acceleration to handle the increased computational demand efficiently.

These fully connected layers were essential for AlexNet’s ability to turn high-level visual features into accurate predictions, helping it excel in classifying 1000 diverse image categories.

5. Dropout and Regularization

A figure displaying the effect of applying the dropout process on a simple neural network [5]

A critical innovation in AlexNet was its use of dropout, a regularization technique that played a key role in improving the model’s ability to generalize to unseen data. Dropout, combined with other regularization strategies, helped AlexNet excel in large-scale image classification tasks.

Dropout

Function

Dropout works by randomly "dropping" a proportion of neurons during training, effectively setting their activations to zero. This prevents neurons from becoming too reliant on specific combinations of other neurons, avoiding complex co-adaptations. As a result, the model learns more independently useful features that generalize better to new data.

Implementation in AlexNet

• Dropout was applied to the first two fully connected layers of the network.

• A dropout rate of 50% was used, meaning half of the neurons were randomly deactivated during each training iteration.

Benefits

1. Reduced Overfitting: By breaking co-adaptations between neurons, dropout reduces the likelihood of overfitting, even with a large number of parameters.

2. Ensemble Effect: Dropout mimics the process of training multiple networks with shared weights, creating a powerful ensemble-like effect that improves performance.

3. Improved Generalization: The model becomes more robust, learning features that work well across various subsets of neurons, improving its performance on unseen data.

Other Regularization Techniques

In addition to dropout, AlexNet employed several other regularization strategies to boost performance and prevent overfitting:

1. Data Augmentation: By applying transformations like random crops, horizontal flips, and color jittering to the input images, the model was exposed to a more diverse set of training examples, further improving its ability to generalize.

2. Weight Decay: AlexNet used L2 regularization, also known as weight decay, to penalize large weights. This encouraged the model to learn simpler representations and reduced the risk of overfitting.

Impact on AlexNet's Performance

The combination of dropout and other regularization techniques was essential to AlexNet’s success:

• Overfitting Reduction: Despite having 60 million parameters, dropout helped control overfitting, ensuring the model could effectively learn from the 1.2 million images in the training set.

• Improved Accuracy: These regularization techniques contributed to AlexNet’s superior generalization ability, leading to significant improvements in top-1 and top-5 error rates on the ImageNet dataset.

Simply put. By employing innovational dropout and other regularization strategies, AlexNet set new benchmarks for image classification, helping to define modern deep learning practices.

6. GPU Acceleration and Parallel Processing

One of the key factors behind AlexNet's breakthrough performance was its efficient use of GPU acceleration. This section explores how AlexNet leveraged graphics processing units (GPUs) to dramatically speed up training and inference.

The Need for GPU Acceleration

AlexNet's architecture, with its 60 million parameters and 650,000 neurons, presented a significant computational challenge. Training such a large network on the ImageNet dataset, which contains over 1.2 million images, would have been impractical using traditional CPU-based computing.

GPU Architecture and Advantages

Graphics Processing Units (GPUs) are designed for parallel processing, making them ideal for the matrix multiplications that dominate neural network computations.

Key advantages of GPUs for deep learning:

1. Massive Parallelism: GPUs have thousands of cores, allowing for simultaneous computations.

2. High Memory Bandwidth: Faster data transfer between memory and processing units improves efficiency.

3. Specialized for Matrix Operations: GPUs are optimized for the types of calculations common in neural networks, particularly matrix operations.

AlexNet's GPU Implementation

AlexNet was implemented across two NVIDIA GTX 580 GPUs, each with 3GB of memory. This dual-GPU setup was necessary due to memory constraints and became a defining feature of the architecture.

Key aspects of AlexNet's GPU implementation:

1. Split Architecture: The network was divided across two GPUs, with some layers spanning both GPUs and others contained within a single GPU.

2. Cross-GPU Communication: Communication between GPUs was minimized and only occurred at certain layers, reducing the overhead.

3. Parallelized Training: AlexNet used batch processing to fully utilize the computational power of the GPUs, speeding up training.

CUDA and Impact on Training Speed

Now you’re probably wondering. How did they effectively leverage the power of these GPUs? Well, AlexNet's GPU acceleration was implemented using NVIDIA's CUDA (Compute Unified Device Architecture) framework.

The development of custom CUDA kernels and use of CUDA was instrumental in achieving the training speed that made AlexNet feasible. By leveraging GPU parallelism, AlexNet was trained in just 5-6 days—compared to the weeks it would have taken on CPUs. This successful application of CUDA for deep learning helped spark wider adoption of GPU computing in AI research.

The use of GPU acceleration, combined with CUDA, dramatically reduced the time required to train AlexNet:

• Training took aforementioned 5 to 6 days on two GTX 580 GPUs.

• This was approximately 10 times faster than what could be achieved on an equivalent CPU setup.

Spoiler alert: This statement highlights the remarkable advancements in computing power since the introduction of AlexNet. In Part 2 of this mini-series, we will demonstrate this progress by coding and training the AlexNet model from scratch using PyTorch. By utilizing modern NVIDIA GPUs such as the A100 or H100, we can now train the model in several hours instead of the multiple days it originally required.

7. Loss Function and Optimization

The choice of loss function and optimization algorithm played a pivotal role in AlexNet’s training process and its ultimate performance. This chapter explores these critical components and how they were implemented in AlexNet to ensure effective training on large-scale data.

Loss Function: Cross-Entropy Loss

AlexNet used the cross-entropy loss function (also known as log loss), which is particularly well-suited for multi-class classification problems like ImageNet.

Mathematical Definition

For a single training example, the cross-entropy loss is defined as:

\(L = -\sum_{i} y_i \log(p_i) \)

Where:

• y​: is the true label (1 for the correct class, 0 for others)

• p: is the predicted probability for each class

Advantages of Cross-Entropy Loss

1. Penalizes confident misclassifications: Cross-entropy heavily penalizes wrong predictions when the model is overly confident, ensuring it corrects quickly in such cases.

2. Smoother Gradients: Compared to other loss functions, cross-entropy provides smoother gradients, leading to more stable convergence during training.

3. Works well with Softmax: Cross-entropy pairs naturally with the softmax activation in the output layer, making it ideal for multi-class classification tasks.

Optimization Algorithm: Stochastic Gradient Descent (SGD) with Momentum

AlexNet employed Stochastic Gradient Descent (SGD) with momentum, a powerful optimization technique that accelerates convergence by incorporating information from previous gradients.

SGD with Momentum Update Rule

The update rule for SGD with momentum is as follows:

\(v = \mu v - \alpha \nabla L(\theta) \)

\(\theta = \theta + v \)

Where:

• v is the velocity (initially set to 0)

• μ is the momentum coefficient (typically 0.9 in AlexNet)

• α is the learning rate

• ∇L(θ) is the gradient of the loss function with respect to the parameters θ\thetaθ

• θ represents the model parameters

Momentum helps accelerate SGD in the direction of consistent gradients, while dampening oscillations in directions with high variance, resulting in faster and smoother convergence.

Key Hyperparameters in AlexNet

1. Learning Rate: Initially set to 0.01 and reduced by a factor of 10 when validation error plateaued.

2. Momentum: Set to 0.9 to balance speed and stability during optimization.

3. Weight Decay: Set to 0.0005, an L2 regularization method that prevents the model from overfitting by penalizing large weights.

Training Process

To train AlexNet efficiently, the following training setup was employed:

1. Batch Size: 128 examples per batch, allowing for efficient computation while keeping memory usage manageable.

2. Epochs: Training was conducted for around 90 epochs, long enough to fully converge on the ImageNet dataset.

3. Learning Rate Schedule: The learning rate was manually reduced 3 times during training, each time by a factor of 10, ensuring the model could fine-tune its weights as it approached convergence.

AlexNet's Overall Architecture and Layer Breakdown

An illustration of the architecture of AlexNet CNN, explicitly showing the delineation of responsibilities between the two GPUs. One GPU runs the layer-parts at the top of the figure while the other runs the layer-parts at the bottom. The GPUs communicate only at certain layers. [6]

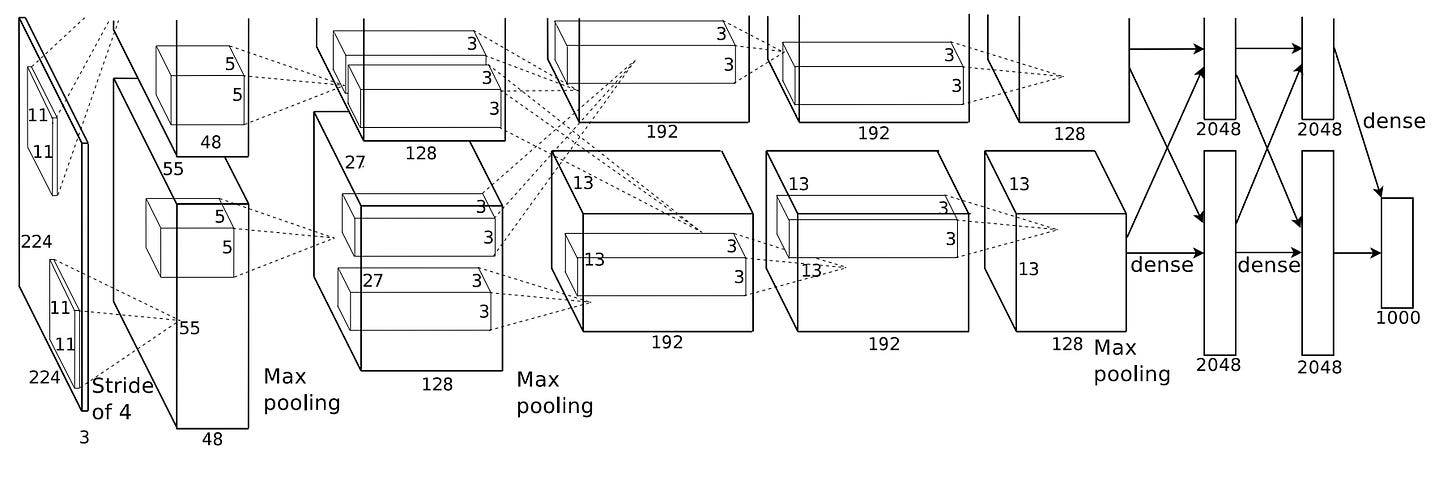
AlexNet’s architecture was a groundbreaking leap forward, introducing depth, complexity, and innovations that have shaped modern deep learning models. This chapter provides a detailed breakdown of its architecture and highlights the key aspects that contributed to its success.

Overall Structure

AlexNet consists of eight layers: five convolutional layers followed by three fully connected layers. Due to memory limitations, the network was split across two GPUs, which allowed the model to efficiently handle its 60 million parameters and 650,000 neurons.

Layer-by-Layer Breakdown

Input Layer

• Dimensions: 227x227x3 (RGB image)

• Preprocessing: Images are resized to 256x256, then randomly cropped to 227x227.

Convolutional Layers

• Layer 1: 96 filters of size 11x11x3 with stride 4, followed by ReLU, Local Response Normalization (LRN), and max pooling.

• Layer 2: 256 filters of size 5x5x48, followed by ReLU, LRN, and max pooling.

• Layer 3: 384 filters of size 3x3x256, followed by ReLU.

• Layer 4: 384 filters of size 3x3x192, followed by ReLU.

• Layer 5: 256 filters of size 3x3x192, followed by ReLU and max pooling.

Fully Connected Layers

• Layer 6 (FC1): 4096 neurons, followed by ReLU and dropout (0.5).

• Layer 7 (FC2): 4096 neurons, followed by ReLU and dropout (0.5).

• Layer 8 (Output): 1000 neurons, followed by softmax to produce class probabilities.

Key Architectural Features

1. Depth: AlexNet's eight layers allowed for more complex feature hierarchies, enabling it to learn richer, more abstract representations.

2. ReLU Activation: Applied after every convolutional and fully connected layer (except the output), ReLU accelerates training and mitigates the vanishing gradient problem.

3. Local Response Normalization (LRN): Applied after the first two convolutional layers, LRN helps improve generalization.

4. Overlapping Max Pooling: Reduces spatial dimensions while preserving important features, applied after the first two layers and the fifth convolutional layer.

5. Dropout Regularization: Used in the fully connected layers with a rate of 0.5, dropout helps prevent overfitting.

6. GPU Split: AlexNet was split across two GPUs to handle the model's memory demands, with layers 1, 2, and 5 spanning both GPUs, while layers 3 and 4 remained on individual GPUs.

Parameter Count

• Total Parameters: Approximately 60 million, with most of them located in the fully connected layers (about 58 million).

Training Process

• Batch Size: 128 examples per batch.

• Epochs: Training continued for approximately 90 epochs.

• Optimizer: Stochastic Gradient Descent (SGD) with momentum.

• Learning Rate Schedule: The learning rate started at 0.01 and was manually reduced when the validation error plateaued.

Impact of the Architecture

AlexNet’s architecture played a crucial role in establishing convolutional neural networks as a dominant paradigm for image recognition. Its ability to train on the massive ImageNet dataset using GPU acceleration, deep architectures, and effective regularization techniques demonstrated the power of deep learning on a large scale.

AlexNet’s victory in the 2012 Image<Net competition set a new benchmark in the field, proving that deep learning could excel where traditional methods had plateaued. Its combination of ReLU activations, dropout, innovative loss function and optimization alogirthm approach, and GPU acceleration has since become standard practice in neural network design.

Conclusion

With AlexNet, we explored a model that not only broke new ground in computer vision but also sparked the deep learning revolution that continues to transform artificial intelligence today. By integrating depth, innovative activation functions, regularization techniques, and GPU acceleration, AlexNet laid the foundation for the future of neural network architectures.

This marks the conclusion of Part 1 of our exploration into AlexNet. We’ve dissected the architecture, understood its training process, and learned about the key innovations that contributed to its success.

But theory alone is just the beginning. In Series 2, we’ll bring AlexNet to life through practical coding. Using PyTorch, we’ll implement the network from scratch, dive deeper into its inner workings, and train it on real datasets. Stay tuned for hands-on learning, as we transition from theory to practice!

Thank you for joining this journey through AlexNet's architecture, and I look forward to seeing you in the next series, where we’ll code, experiment, and learn by doing.

Citations

[1] AlexNet and ImageNet: The birth of Deep Learning. (n.d.). Pinecone. https://www.pinecone.io/learn/series/image-search/imagenet/

[2] Yani, M., S, S. M. B. I., & ST, M. C. S. (2019). Application of transfer learning using convolutional neural network method for early detection of Terry’s nail. Journal of Physics Conference Series, 1201(1), 012052. https://doi.org/10.1088/1742-6596/1201/1/012052

[3] Baheti, P. (2024, July 2). Activation Functions in Neural Networks [12 Types & Use Cases]. V7. https://www.v7labs.com/blog/neural-networks-activation-functions

[4] Luna, K., Klymko, K., & Blaschke, J. P. (2021). Accelerating GMRES with Deep Learning in Real-Time. arXiv (Cornell University). https://doi.org/10.48550/arxiv.2103.10975

[5] Khalifa, A. B., & Frigui, H. (2016, October 17). Multiple instance fuzzy inference neural networks. arXiv.org. https://arxiv.org/abs/1610.04973

[6] Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). ImageNet Classification with Deep Convolutional Neural Networks. https://papers.nips.cc/paper_files/paper/2012/hash/c399862d3b9d6b76c8436e924a68c45b-Abstract.html